2021年8月4日，北京大学数学科学学院教授、大数据分析与应用技术国家工程实验室主任张平文院士，北京国际数学研究中心张磊副教授与浙江大学数学科学学院王伟研究员合作，在Acta Numerica发表题为“Modelling and Computation of Liquid Crystals”的综述论文。

液晶是一种介于液体和晶体之间的软物质。过去四十年液晶的研究取得了巨大的进展，不仅极大地促进了基础科学研究，同时在工业上得到了广泛的应用。液晶已有很多数学和物理模型描述其多相结构、缺陷和动力学行为，例如Onsager分子模型，Landau-de Gennes张量模型，Ericksen-Leslie向量模型等。这些模型的数学理论、相互关系以及计算是重要的数学问题。

论文首先介绍了液晶三类不同层次的数学模型及其联系，即分子模型、张量模型和向量模型。这些模型或者是力学家根据力学原理和本构假设建立的，或者是物理学家基于分子结构运用统计物理平均场理论建立的。以液晶不同模型之间的关系为重点，运用模型约简方法，可以从严格数学意义上或形式上建立不同模型之间联系，并综述了相关的理论分析结果(图一)。

图一:从微观分子理论到宏观连续理论的模型约简

论文接下来介绍了液晶的计算方法，包括计算液晶稳定缺陷的能量极小化方法和梯度流方法，以及液晶流体动力学模型的数值方法，并列举了各类受限在不同几何区域和条件下向列相液晶的缺陷构型。由于液晶通常具有多个有序相，那么如何通过计算找出所有的相以及不同相之间的连接关系？论文先回顾了计算过渡态和转移路径的计算方法，例如寻找最小能量路径的弦方法；然后介绍了近年来提出的解景观概念，及利用鞍点动力学构建解景观的计算方法，同时给出了二维受限区域内向列相液晶完整的解景观(图二)。

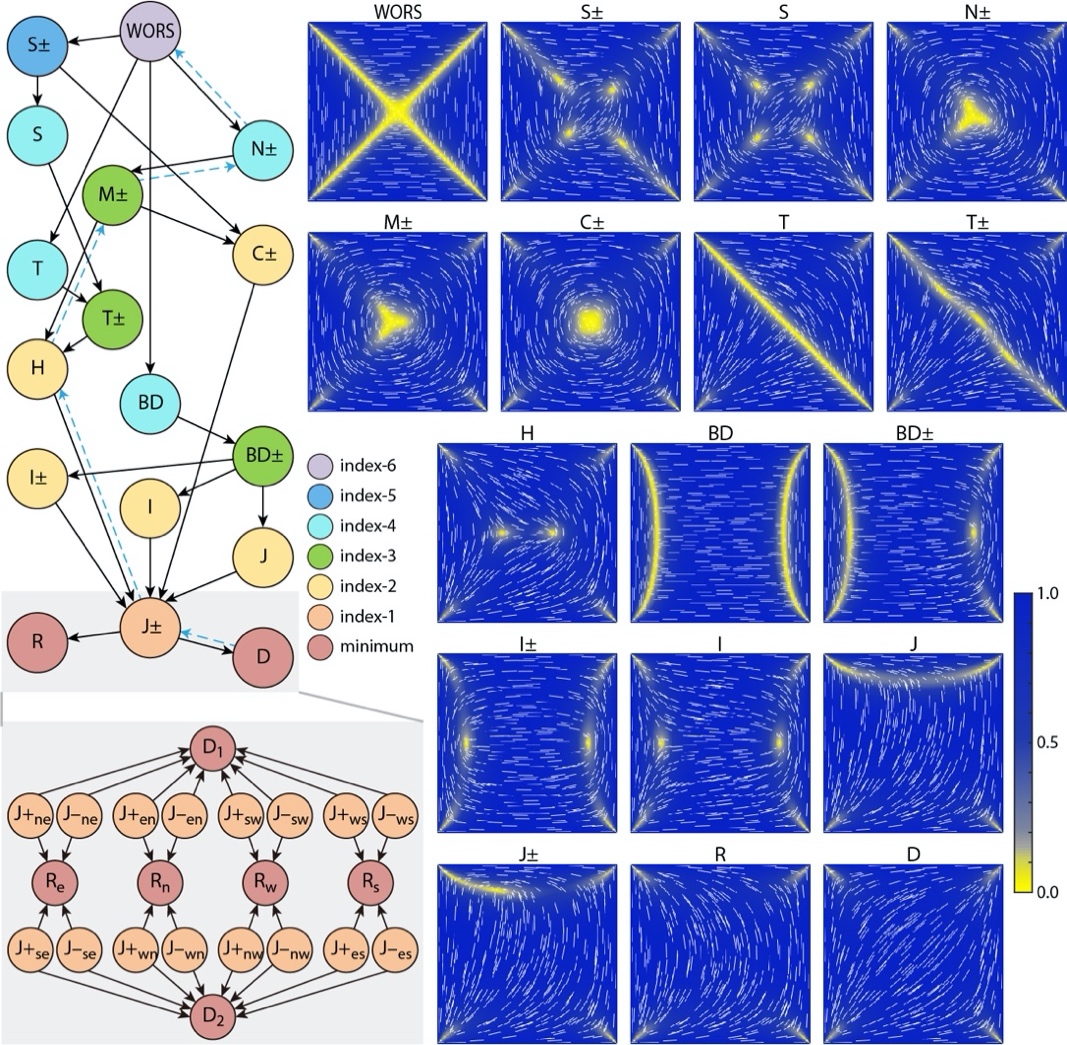
图二:受限在方形区域中向列相液晶的解景观

论文最后总结了液晶的研究主要关注分子的拓扑和几何特征如何影响介观结构，从而决定液晶材料的性质。液晶的科学价值不仅在于提出新的数学问题，而且促进了新的研究方法。同时，论文对液晶的未来研究提出了一些展望，包括液晶平衡解的对称性，动力学模型的适定性和长时间行为，复杂受限液晶系统的解景观，多相及活性液晶系统的相变等问题。

Acta Numerica是数值分析与科学计算领域的顶级综述期刊(数学类影响因子最高的期刊)。该期刊1992年创刊，每年邀请领域内著名专家撰写综述论文，每年只出版一期，每期发表6-8篇文章。该论文是首篇由中国内地高校独立完成的文章。该工作得到了国家自然科学基金委和英国皇家学会牛顿高级学者的资助。

论文作者介绍:

张平文，北京大学数学科学学院教授，中国科学院院士，发展中国家科学院院士，美国工业与应用数学会会士。现任北京大学党委常委、北京大学副校长、大数据分析与应用技术国家工程实验室主任、北京大学大数据科学研究中心主任、中国工业与应用数学学会理事长。担任学术期刊《CSIAM Trans. Appl. Math》主编以及十余种国内外期刊的编委。主要从事复杂流体的数学理论和计算方法、移动网格方法及其应用、人工智能的数学理论、大数据分析与应用等方面的研究，曾获国家自然科学二等奖、教育部高等学校自然科学一等奖、国家杰出青年基金资助、冯康科学计算奖等多项荣誉。2011年在第七届国际工业和应用数学大会作大会邀请报告，2014年在美国工业和应用数学年会作大会邀请报告，2015年担任第八届国际工业和应用数学大会组织委员会成员及学术子委员会主席，2018年国际数学家大会45分钟邀请报告人。

张磊，北京大学北京国际数学研究中心长聘副教授/研究员，定量生物学中心PI。主要研究领域为计算和应用数学，包括稀有事件与解景观的算法与应用，计算系统生物学，计算材料科学等。研究成果在Phys.Rev.Lett.,SIAM系列, Cell子刊等期刊发表。曾获中组部高层次青年人才计划、基金委优秀青年科学基金、英国皇家学会牛顿高级学者、基金委原创探索计划等项目资助。现任SIAM J. Appl. Math, CSIAM Trans. Appl. Math, DCDS-B，The Innovation，计算数学等期刊编委。

王伟，浙江大学数学科学学院长聘副教授/研究员，2013年博士毕业于北京大学数学科学学院，导师为张平文教授。主要研究领域为应用分析与偏微分方程，包括液晶数学理论，流体自由边值问题等，研究成果在Comm. Pure Appl. Math., Arch. Ration. Mech. Anal, J. Funct. Anal.等期刊发表，曾入选中国科协“青年人才托举工程”，获基金委优秀青年科学基金等项目资助。